Menu
Mark Up, Discount and Profit questions confuse a lot of people. But, actually, most of them are absolute sitters — very easy to solve — a free ride! How? We will just see. Let me begin with the previous post’s question.
Question: If a retailer marks up an article by 40% and then offers a discount of 10%, what is his percentage profit?
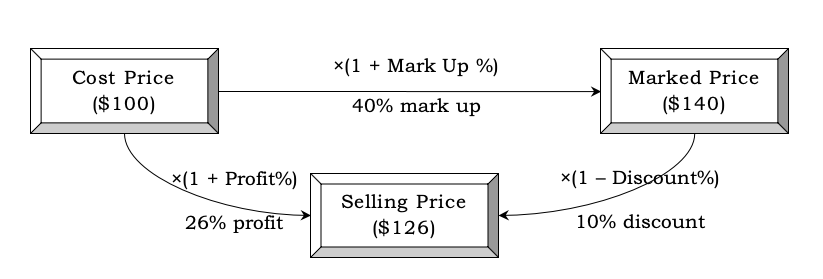
Let us say the retailer buys the article for €100 (€100 is his cost price of the item). He marks it up by 40% i.e. increases his cost price by 40% (
) and puts a tag of €140 on the article. Now, the article remains unsold and he puts it on sale – 10% off everything. So the article marked at €140, gets €14 off and sells at €126 (because 
). This €126 is the selling price of the article. To re-cap, we obtained this selling price in the following way:
Cost Price 
(1 + Mark Up%) (1 – Discount%) 
Selling Price
The profit made on the item is €26 (obtained by subtracting 100, the retailer’s cost price, from 126, the retailer’s selling price).
He got a profit % of 
% 
Or we can say that Cost Price (1 + Profit%) = 
Selling Price
The above shows the two ways in which you can reach the selling price: using mark-up and discount or using profit. The same thing is depicted in the diagram below:
Therefore, Cost Price (1 + Mark Up%) (1 – Discount%)= Cost Price (1 + Profit%)
Or
(1 + Mark Up%) (1 – Discount%)= (1 + Profit%)
Look at the numbers here: Mark Up: 40%, Discount: 10%, Profit: 26% (Not 30% that we might expect because 40% – 10% = 30%)
Why? Because the discount offered was on €140, not on €100. So a bigger amount of €14 was reduced from the price. Hence the profit decreased. This leads us to an extremely important question in percentages – What is the base? 100 was increased by 40% but the new number 140 was decreased by 10%. So in the two cases, the bases were different. Hence, you cannot simple subtract 10 from 40 and hope to get the Profit %. Also, mind you, almost certainly, 30% will be one of the answer choices, albeit incorrect. (The GMAT doesn’t forego even the smallest opportunity of tricking you into making a mistake!)
Let’s see this concept in action on a tricky third party question.
A dealer offers a cash discount of 20%. Further, a customer bargains and receives 20 articles for the price of 15 articles. The dealer still makes a profit of 20%. How much percent above the cost price were his articles marked?
a) 
%
b) 
%
c) 
%
d) 
%
e) 
%
This question involves two discounts:
1. the straight 20% off
2. discount offered by selling 20 articles for the price of 15 – a discount of cost price of 5 articles on 20 articles i.e. a discount of 
%
Using the formula given above:
m = 100
Therefore, the markup was 100%.
Answer (A).
Note: The two discounts are successive percentage discounts.
Learn a streamlined way to tackle percentage questions using basic logic, not lengthy formulas.
https://anaprep.com/arithmetic-simple-approach-to-percentages/
Understand how to handle chained percentage increases or decreases the smart way – one clear step at a time.
https://anaprep.com/arithmetic-successive-percentage-changes/
Break free from tedious calculation by using conceptual shortcuts that simplify tricky problems with speed.
https://anaprep.com/using-conceptual-methods-to-solve-hard-questions-with-ease-and-speed-on-gmat/
Decode cost price, selling price, and profit questions with a clear, structured breakdown for quick mastering.
https://anaprep.com/arithmetic-the-concept-of-cost-price/
Tackle a tough problem that merges ratios and percentages – a great exercise to boost your quant accuracy.
https://anaprep.com/arithmetic-ratios-and-percentages-problem-going-from-48-to-51/