
Today, let’s discuss the relative placements of exponents on the number line.
We know what the graph of ![]() looks like:
looks like:
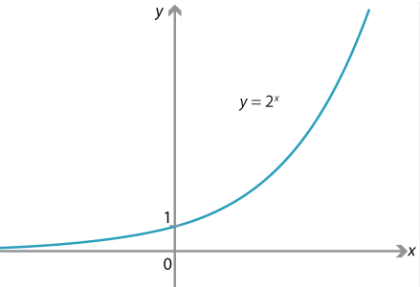
It shows that when ![]() is positive, with increasing value of
is positive, with increasing value of ![]() ,
, ![]() increases very quickly (look at the first quadrant), but we don’t know exactly how it increases.
increases very quickly (look at the first quadrant), but we don’t know exactly how it increases.
It also shows that when ![]() is negative,
is negative, ![]() stays very close to 0. As
stays very close to 0. As ![]() decreases, the value of
decreases, the value of ![]() decreases by a very small amount.
decreases by a very small amount.
Now note the spacing of the powers of 2 on the number line:

![]()
![]()
![]()
![]()
and so on…
![]()
![]()
![]()
![]()
So every power of 2 is equidistant from 0 and the next power. This means that a power of 2 would be much closer to 0 than the next higher powers. For example, ![]() is at the same distance from 0 as it is from
is at the same distance from 0 as it is from ![]() .
.
But ![]() is much closer to 0 than it is to
is much closer to 0 than it is to ![]() ,
, ![]() etc.
etc.
Let’s look at a question based on this concept. Most people find it a bit tough if they do not understand this concept:
Question: Given that ![]() , which of the following values for
, which of the following values for ![]() yields the lowest value for |
yields the lowest value for |![]() |?
|?
A) 35
B) 90
C) 91
D) 95
E) 105
We need the lowest value of |![]() |. We know that the smallest value any absolute value function can take is 0. So
|. We know that the smallest value any absolute value function can take is 0. So ![]() should be as close as possible to (
should be as close as possible to (![]() ) to get the lowest value of |
) to get the lowest value of |![]() |.
|.
Let’s try to simplify:
(![]() )
)
![]()
![]()
Which value should ![]() take such that
take such that ![]() is as close as possible to
is as close as possible to ![]() ?
?
![]() is obviously larger than
is obviously larger than ![]() . But is it closer to
. But is it closer to ![]() or
or ![]() or higher powers of 2?
or higher powers of 2?
Let’s use the concept we have learned today – let’s compare ![]() with
with ![]() and
and ![]() .
.
![]()
![]()
So now if we compare these two with ![]() , we need to know whether
, we need to know whether ![]() is closer to 0 or closer to
is closer to 0 or closer to ![]() .
.
We already know that ![]() is equidistant from 0 and
is equidistant from 0 and ![]() , so obviously it will be much closer to 0 than it will be to
, so obviously it will be much closer to 0 than it will be to ![]() .
.
Hence, ![]() is much closer to
is much closer to ![]() than it is to
than it is to ![]() or any other higher powers.
or any other higher powers.
We should take the value 90 to minimize |![]() |, therefore the answer is (B).
|, therefore the answer is (B).