Mark Up, Discount and Profit questions confuse a lot of people. But, actually, most of them are absolute sitters — very easy to solve — a free ride! How? We will just see. Let me begin with the previous post’s question.
Question: If a retailer marks up an article by 40% and then offers a discount of 10%, what is his percentage profit?
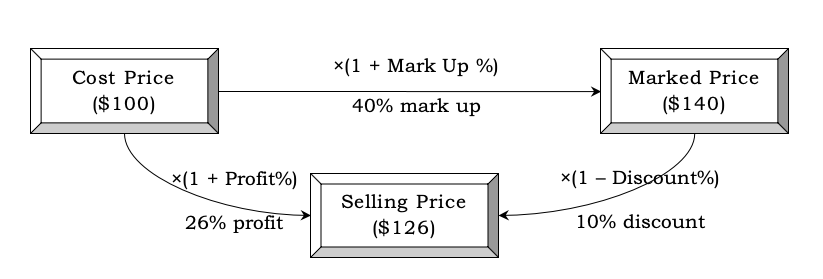
Let us say the retailer buys the article for €100 (€100 is his cost price of the item). He marks it up by 40% i.e. increases his cost price by 40% () and puts a tag of €140 on the article. Now, the article remains unsold and he puts it on sale – 10% off everything. So the article marked at €140, gets €14 off and sells at €126 (because
). This €126 is the selling price of the article. To re-cap, we obtained this selling price in the following way:
Cost Price (1 + Mark Up%)
(1 – Discount%)
Selling Price
The profit made on the item is €26 (obtained by subtracting 100, the retailer’s cost price, from 126, the retailer’s selling price).
He got a profit % of %
Or we can say that Cost Price (1 + Profit%) =
Selling Price
The above shows the two ways in which you can reach the selling price: using mark-up and discount or using profit. The same thing is depicted in the diagram below:
Therefore, Cost Price (1 + Mark Up%)
(1 – Discount%)= Cost Price
(1 + Profit%)
Or
(1 + Mark Up%) (1 – Discount%)= (1 + Profit%)
Look at the numbers here: Mark Up: 40%, Discount: 10%, Profit: 26% (Not 30% that we might expect because 40% – 10% = 30%)
Why? Because the discount offered was on €140, not on €100. So a bigger amount of €14 was reduced from the price. Hence the profit decreased. This leads us to an extremely important question in percentages – What is the base? 100 was increased by 40% but the new number 140 was decreased by 10%. So in the two cases, the bases were different. Hence, you cannot simple subtract 10 from 40 and hope to get the Profit %. Also, mind you, almost certainly, 30% will be one of the answer choices, albeit incorrect. (The GMAT doesn’t forego even the smallest opportunity of tricking you into making a mistake!)
Let’s see this concept in action on a tricky third party question:
A dealer offers a cash discount of 20%. Further, a customer bargains and receives 20 articles for the price of 15 articles. The dealer still makes a profit of 20%. How much percent above the cost price were his articles marked?
a) %
b) %
c) %
d) %
e) %
This question involves two discounts:
1. the straight 20% off
2. discount offered by selling 20 articles for the price of 15 – a discount of cost price of 5 articles on 20 articles i.e. a discount of %
Using the formula given above:
m = 100
Therefore, the markup was 100%.
Answer (A).
Note: The two discounts are successive percentage discounts.

Founder, sole curriculum creator and webinar instructor for ANA PREP, Karishma has been working in the test prep industry for almost 20 years now, of which 15+ are in GMAT exam preparation. She is an expert of Quant, Verbal and Data Insights and is known for her simple and elegant solutions. Her venture, ANA PREP, is one of the best GMAT online coaching platforms. Contact her at karishma@anaprep.com