Drawing Extreme Diagrams | Geometry

Let’s continue with geometry today. We would like to discuss how drawing extreme diagrams can help you solve questions. Most GMAT questions are quite intuitive and hence our non-traditional methods are perfect for them. They are not typical MATH problems per se; instead, they are logical puzzles. If you can prove why some things will not work, it means whatever is left will work.

Let me explain with the help of an official Data Sufficiency question.

Question:

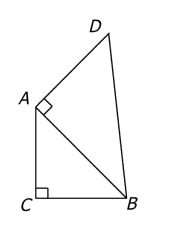
In the figure above, is the area of the triangle ${ABC}$ equal to the area of the triangle ${ADB}$ ?

Statement 1: ${{AC}^2=2{AD}^2}$

Statement 2: Triangle ${ABC}$ is isosceles.

Solution:

When presented with this question, people see right triangles and jump to Pythagorean theorem, isosceles triangles and then wage a war on $AC$ , $AB$ , $CB$ and $AD$ relations. Well, that is our traditional approach. But what do we do if making equations and solving for relations isn’t our style?

We make diagrams and figure out the relations! One thing that is apparent the moment we read statement 1 is that the figure is not to scale. From the figure it looks as if $AD$ is greater than or at best, equal to $AC$ . That itself is an indication that if you draw the figure on your own, you could see something that will make this question very simple. The question setter doesn’t want to show you that and hence he made the distorted figure.

Anyway, let’s first analyze the question. Then we will look at the statements.

We need to compare areas of $ABC$ and $ADB$ . Both are right angled triangles.

$Area\ of\ ABC = \frac{1}{2} \times AC \times BC$

$Area\ of\ ADB = \frac{1}{2} \times AD \times AB$

We need to figure out whether these two are the same.

Think about it this way – we are given a triangle $ABC$ with a particular area. So the length of $AD$ must be defined. If $AD$ is very small, (shown by the dotted lines in the diagram given below) the area of $ADB$ will be very close to 0. If $AD$ is very large, the area will be much larger than the area of $ABC$ . So for only one value of $AD$ , the area of $DAB$ will be equal to the area of $ABC$ .

We need to figure out whether for the given relations, the triangles have equal area.

Statement 1: ${AC}^2=2{AD}^2$

This gives us $AD = \frac{AC}{\sqrt 2}$ . Let’s draw $AC$ and $AD$ such that $AD$ is somewhat shorter than $AC$ . Now can we say that the areas of the two triangles are the same? No. The area of $ABC$ is decided by $AC$ and $BC$ both not just $AC$ . We can vary the length of $BC$ to see that the relation between $AC$ and $AD$ is not enough to say whether the areas will be the same (see the diagrams given below).

So this statement alone is not sufficient.

Statement 2: Triangle $ABC$ is isosceles.

This means that $AC = BC$ . Notice that the triangle is right angled so the hypotenuse must be the largest side. If $ABC$ is isosceles, it means that the two legs of the triangle must be equal. Hence sides of $ABC$ must be in the ratio $1 : 1 : \sqrt2 = AC : BC : AB$ .