Innovative Question on Rotation | Geometry

If you have run through the Co-ordinate Geometry module, then you must check out this question. It may be beyond GMAT level but it tests the GMAT relevant concepts in a most innovative way.

Question: Triangles ${ABC}$ and ${ADE}$ have areas 2007 and 7002, respectively, with ${B = (0, 0)}$ , ${C = (223, 0)}$ , ${D = (680, 380)}$ , and ${E = (689, 389}$ ). What is the sum of all possible ${x}$ -coordinates of ${A}$ ?

(A) 282

(B) 300

(D) 900

(E) 1200

Solution:

The worse the numbers given, the more the probability that they will not get used at all.

Draw a diagram. $BC$ lies on $x$ axis. To make a triangle with a given area (2007) i.e. a fixed altitude (whatever that may be, it is 18 in this case), $A$ will lie on any point on the two red lines. The two red lines are 18 units above and below the $x$ axis. Think about this before moving ahead.

Now draw $DE$ . To make a triangle with a given area (7002) i.e. a fixed altitude (whatever that may be), $A$ will lie on any point on the two given dotted purple lines.

So what we need is the $x$ co-ordinates of the 4 possible $A$ values ( $A'$ , $A''$ , $A'''$ and $A''''$ )

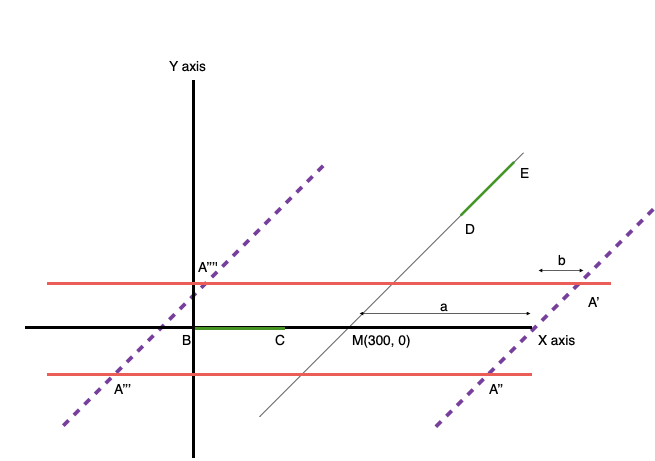
Now notice the co-ordinates of $D$ and $E$ are $D = (680, 380)$ , and $E = (689, 389)$ . So the diff between $x$ co-ordinates is 9 and between $y$ co-ordinates is also 9. This means $DE$ is a line with slope 1.

Hence, it will cut the $x$ axis at 300 (when we move y co-ordinate 380 units down, we will move the $x$ co-ordinate 380 units to the left so the $x$ co-ordinate will become 680 – 380 = 300). This is the point $M$ .