
Normally, people will say – Never! But we beg to differ.
Often, you would have read in our posts or heard us talk about the importance of diagrams in many Quant questions – Co-ordinate geometry, Races, some Time-Speed-Distance problems, Sets problems etc. We suggest you make diagrams when not given in many such questions. But sometimes, test makers give such diagrams that we wish we were not given the diagram at all. In fact, the addition of a diagram, something that often simplifies our question, takes the difficulty of the question to a whole new level. By now you are probably thinking that I am surely exaggerating!
So let me show you what I mean using an official question.
Try to figure this out: When the figure given below is cut along the solid lines, folded along the dashed lines, and taped along the solid lines, the result is a model of a geometric solid.
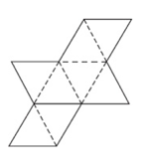
Now, can you use your imagination and figure out what kind of a geometric solid you will get in this case? Don’t go ahead just yet.
First give it a shot for a few minutes.
To be honest, I have given it a try and it is certainly not easy. I will know for sure only when I actually carry out the mentioned steps – cut the paper along the solid lines, fold along the dashed lines and then tape up along the solid lines. Without carrying out the steps I am not sure exactly what kind of a figure I will get.
So the test maker comes to our rescue here. Here is the complete question:
Question: When the figure above is cut along the solid lines, folded along the dashed lines, and taped along the solid lines, the result is a model of a geometric solid. This geometric solid consists of two pyramids each with a square base that they share. What is the sum of number of edges and number of faces of this geometric solid?
(A) 10
(B) 18
(C) 20
(D) 24
(E) 25
The test maker specifies what kind of a figure we get – two pyramids, each with a square base that they share. Figuring this out in a minute without an actual paper and scissor at hand would need extraordinary skill. Many test takers spend precious minutes trying to make sense of the given diagram. Instead, it should be completely ignored! We already know what it will look like – two pyramids with a common square base. This, we understand! We know what a pyramid looks like – triangular faces converge to a single point at the top with a polygon (often a square) base. We need two pyramids joined together at the base.
This is what the solid will look like.
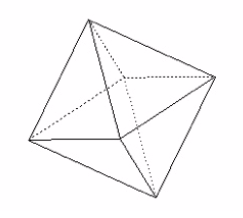
Just the 4 triangular faces of the two pyramids will be visible. Since they will share the square base, the base will not be visible.
Hence, the figure will have 8 faces.
Now let’s see how many edges there will be: To make the top pyramid, four triangular faces join to give four edges. To make the bottom pyramid, four triangular faces join to give four more edges. The two pyramids join on the square base to give another four edges.
So all in all, we have 4 + 4 + 4 = 12 edges
When we sum up the faces and edges, we get 8 + 12 = 20
The question is much more manageable now. All we had to do was ignore the diagram given to us!